本课题拟编写线性动力有限元程序，针对平面问题，在均匀材料受静载作用的响应的基础上，通过修改计算过程中离散单元的物理属性值，来实现梯度材料的受载响应计算。通过分步计算不断修正载荷列阵达到材料受动载的响应计算。并实现使用ANSYS建模产生相关文件，使用用户界面显示图形和结果的功能。
本文将功能梯度材料的环形圆筒受内压的模型作为一个算例，计算模型的位移、应力响应情况并作分析。
 2    非均质梯度材料处理
2.1    非均质梯度材料简介
功能梯度材料采用先进的复合材料技术，使材料的组成结构沿厚度方向由一侧向另一侧变化，使用一定技术使材料达到一定的混合要求，使其组成结构随位置坐标缓慢连续变化，从而使材料的性质和功能也呈现梯度变化的新型材料[11]。
功能梯度材料是一种复合材料，其物理属性呈不均匀变化，是位置坐标的函数。当功能梯度材料由两种材料复合时，由下图可知其物理属性连续变化并介于两种材料单独物理属性之间。
 
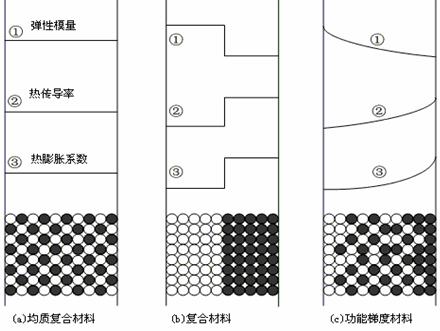
图2.1. 梯度材料示意图（各种材料断面构成和内部特性）
2.2    非均质梯度材料物理属性计算
有限元法是将连续体简化为由有限个单元组成的离散化模型，具有连续变化的非均质梯度材料，在单一单元内是一个随位置坐标变化的值。单元如果足够小，在每个单元上的物理属性可以看作是常量，从而用数值近似处理。
在三角形单元上，根据高斯数值积分，单元上的物理量I：[9]
 化为面积坐标表示时，可根据直角坐标（r,z）和面积坐标的以下关系进行变换：
 而于是 因此由三角形单元上三节点坐标值和其对应物理量值可以得到单元相应平均物理量值。 ANSYS非均质梯度材料圆筒的动态应力的有限元分析(3):http://www.751com.cn/wuli/lunwen_10812.html