- 上一篇:中日《等腰三角形》教学内容对比
- 下一篇:ARMA模型中国人口老龄化发展趋势的预测和分析
2011年版的《数学课程标准》最鲜明的一个特点就是明确提出了“模型思想”这一重要内容。模型思想是数学建模的灵魂和基础。新课标指出,模型思想的建立有利于学生体会和理解数学与实际生活联系,有助于学生发展运用数学的意识,观察生活,感受生活中的数学,建立数学模型,提升学习数学的兴趣。
与此同时,各国数学家和教育家也纷纷提出,数学的教学应该着重于应用。这一点在我国新编的各套数学教材中均有体现:从生活实际渗透知识本质,并将知识运用于实际生活……在这样的背景下,数学建模思想在数学教学中的应用显得尤为重要。
2. 数学模型与数学建模思想
2.1 概念的解释和理解
粗略来讲,数学模型就是针对研究对象的数字特征或数量依存关系,运用形式化的数学符号和数学语言,概括地或近似地表达出来的一个数学结构。广义地说,数学中的各种基本算法及公式和基本概念都可以称为数学模型,由此来讲,小学数学中常见的数学模型有:公式模型、方程模型、集合模型、函数模型等;狭义来说,只有反映特定问题或是特定的具体事物的数学关系结构才能称为数学模型。总的来说,数学模型具有解释、判断、预见三大功能。
数学建模思想是指针对问题构建数学模型,再通过研究数学模型来解决问题的一种数学思想。数学的本质是将问题符号化和公式化,在小学数学中应用数学建模思想,主要用数学建模思想来指导数学的教学——从学生已有的生活经验出发,引导学生经历实际问题抽象成为数学模型的过程,并进行解释和运用,促进学生综合能力的发展,提升学生学习数学的兴趣和应用数学的信心。
2.2 数学建模的基本步骤
一般来说,数学建模分为以下几个基本步骤:
1. 模型准备:分析要解决的实际问题,了解其背景、实际意义,掌握和收集对象的相关信息,包括数据、图表与其他事物的关系等,确定建模的根本目的,用数学语音清晰地描述这个问题。
以小学算术应用题为例:
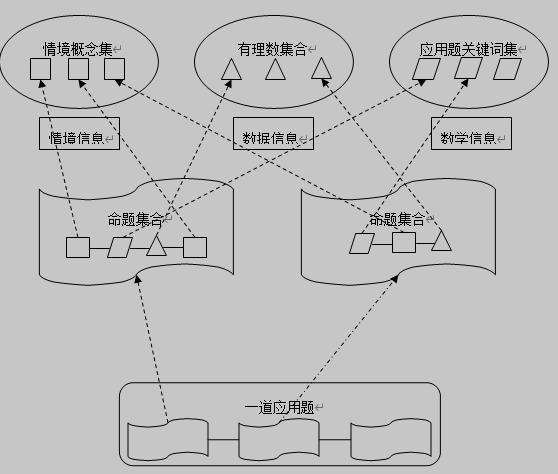
图1 小学算术应用题的信息构成
2. 模型假设:根据所掌握的背景信息和建模的根本目的,对问题进行必要、合理的简化,用精确的语言提出一些恰当的假设。