- 上一篇：基于学情的初中数学变式教学设计平方差公式
- 下一篇：多项式拟合在变形数据分析中的应用
摘要本文讨论了非线性差分方程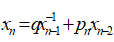 
在满足给定的周期数列 时解的单调性.采用了将非线性问题转换为线性问题的方法，通过严密的思考和细心的推断得出了结论.
该论文有参考文献8篇.69170
毕业论文关键词：差分方程 非线性 单调性
On Monotonicity of Solutions of the Nonlinear DifferenceEquation
Abstract
This paper is concerned with monotonous solution for nonlinear difference equations of ,and are given. Using an approach that making The non-linear problem into linear problem through rigorous thinking and careful inference concluded.
Key Words: Difference Equation Nonlinear Boundedness
目 录
摘要Ⅰ
Abstract-Ⅱ
目录Ⅲ
1 绪论- -1
2主要结果1
3 结论-8
参考文献-9
致谢10
1 绪论
对于阶数 的非线性差分方程：
关于其的讨论在过去的很长时间里都受到人们的重视.一般看来，对此等方程的研究都基于一个前提， 和初始值集合 是给定的.大多研究的对象F是在有理式的情况之下，但是到目前为止，该领域的研究尚未成熟.在文献[3]中，A.M.Amleh 研究了差分方程 解的有界性，赵玉萍在文献[2]中改进了他的研究。文献[4]到[5]都是研究了差分方程的有界性，受到他们的方法的启发，我们用讨论有界性的方法去探究差分方程的单调性.来!自~751论-文|网www.751com.cn
本文研究差分方程：
其初值是 ， ，并且 均为正值，
受到文献[1]的启发，使用相似的变换技巧
(2)
我们将(1)化为线性差分方程
(3)
从而可以讨论方程的解及其有界性.
在文中，为了表达的方便，我们可以约定：当 时， .
2 主要结果
首先我们来求解方程(3).由(2)和(3)， ，我们得到：
n为偶数；
n为奇数. (4)
其次，我们通过(4)来讨论方程(1)的解.在本文的假设条件之下，对于所有的 .会得到：
， (5)
. (6)
定理 2.1 方程(1)的解由(5)或(6)表出.
下面，我们来讨论方程(1)的解的有界性.
为了得到方程(1)的解有界的充分条件，我们首先对 和 的通项表达式进行分析可知：