3.3.1 假设需求函数和供给函数是线性函数
假设需求函数为 ，供给函数为 ，式中，  、  、 和 均为常数，且均大于零.我们有：
 ，
联立以上三个方程可得：
 .
解此差分方程，可得第 期的产品价格为：
 .
当市场价格达到均衡时，有 成立，所以，由 式可得均衡价格为：
 .
将上式代入 式可得：
 .
当 时， ，从而
 .
分析 式，可得：
第一种情况：当 时， ， .如图1所示，相对于价格轴，供给曲线斜率的绝对值小于需求曲线斜率的绝对值.随着时间 的推移，实际价格 将以越来越小的幅度上下波动，最后趋近于均衡价格 .这种类型的蛛网被称为“收敛型蛛网”.
 
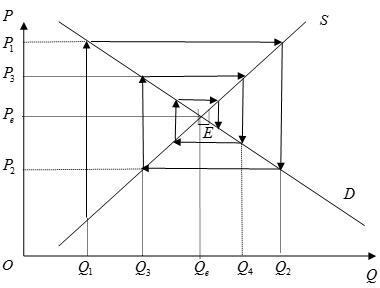
图1  收敛型蛛网
第二种情况：当 时， ， .如图2所示，相对于价格轴，供给曲线斜率的绝对值大于需求曲线斜率的绝对值.随着时间 的推移，实际价格 将以越来越大的幅度上下波动，无穷大地偏离均衡价格 .这种类型的蛛网被称为“发散型蛛网”.
      
图2  发散型蛛网
第三种情况：当 时， 为上下跳动的常数. 如图3所示，相对于价格轴，供给曲线斜率的绝对值等于需求曲线斜率的绝对值.随着时间 的推移，实际价格 将以相同的幅度上下波动，既不偏离也不逼近均衡价格 .这种类型的蛛网被称为“封闭型蛛网”. 市场经济中的数学模型(2):http://www.751com.cn/shuxue/lunwen_21158.html