- 上一篇:CALYPSO的AunCs(n=5-8)的电子结构及特征的理论研究
- 下一篇:纳米机械振子与量子点耦合系统的快慢光效应研究
2 熵函数的导出
2.1 熵函数
依据克劳休斯原理:任意可逆循环过程的热温商之和为零 。其可逆循环过程:A B A如图1所示
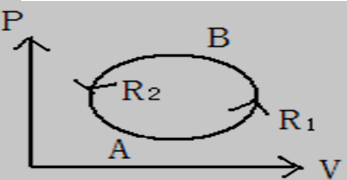
图1.任意可循环过程[5]
因为 (1)
所以 (2)
所以 (3)
(3)式表明: 的值由始态、终态决定,而与A B之间所经过的具体的可逆过程没有任何关系。故 是某一函数的全微分形式,又因为状态函数具备数学上的全微分的性质。即熵函数表示为:
(4)
2.2 熵的意义
1.熵是系统的状态函数,是容量性质,整个系统的熵值是各个部分的熵的总和 。
2.熵是状态函数,但不像温度和压力可凭感觉知道,也不像体积可由实验测知 。
3.熵的特征是在状态发生变化的系统中,系统熵的变化不是因为从始态到终态的实际过程而产生的,而是在始态、终态之间的一个可逆的变化过程,从而这样计算可逆过程的热温熵。
即 (5)
4.熵的性质是在孤立系统中,熵只增加而不减少,并以此作为热力学过程方向与限度的判据。即:
(1) 为自发过程;(2) 为系统处于平衡;(3) 为不能发生的过程。
5.在统计物理学中熵的意义在于它表示了关于分子热运动混乱程度的一种量度(在公式 中k是玻耳兹曼常数, 是热力学几率)。熵增加代表孤立系统内部的过程从几率小的状态向几率大的状态进行,也就是从比较有规则、比较有秩序的状态向更无规则、更无序的状态变化 。总的来说是从不混乱向混乱方向演变。