- 上一篇:基于Android系统的位置推荐系统设计
- 下一篇:基于小波分析算法的红外图像降噪仿真实现
1.2 故障测距理论的研究现状
1.3 暂态行波的处理方法
研究了两种暂态信号处理方法:小波分析,Hilbert-Huang变换。
1.3.1 小波分析的基本思想
处理暂态信号,最主要是对非平稳变化数据序列进行分析,单纯的时域分析和频域分析都无法准确的分析这种信号,所以就产生了时域局部化分析的思想。
时域局部化是一种信号的表示方法,既可以体现信号的整体变化趋势与主体特征,又能够体现信号的局部细节突变程度。傅里叶变换作为一种基本的时域分析法,能够很好地分析平稳信号,但是对于突变信号是就不能正确反映,而在行波测距原理中突变正是我们测量的关键所在,因此我们需要寻找其他分析方法。小波变换源自于傅里叶变换,能够对函数、信号、图像等的任意细节进行分析,在数据压缩、信号的分解与重构、特征提取等一些工程应用中有很好的实际意义[5]。
1.3.2 Hilbert-Huang变换的基本思想
Hilbert-Huang变换(Hilbert-Huang transform,HHT)信号分析法可分为经验模态分解(Empirical Mode Decomposition,EMD)和Hilbert变换两个步骤[6]。
经验模态分解作为HHT的核心部分,其基本原理是将一个非平稳的复杂信号进行分解,分解为多个平稳的信号分量和一个残余量,其中平稳分量代表信号的不同尺度特征,称为本征模函数(Intrinsic Mode Function,IMF),残余量则代表信号的变化趋势。然后再对各IMF分量进行Hilbert变换,得到时间-瞬时频率曲线和时间-瞬时幅值曲线。
不是所有分解后的分量都是IMF分量,只有符合以下两个要求才行:
1) 函数在整个数据序列中,局部极值点和过零点的数目必须相等,或最多相差不大于一个;
2) 在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络(下包络线)的平均值必须为零[7]。
实际上,条件二实质为“数据的局部均值是零”,只是对于非平稳信号,局部均值定义起来比较困难,计算也不简单,故釆用局部极大值包络和局部极小值包络的平均值来代替局部均值,这样就可以让信号的波形局部对称。
1.4 本文的主要工作
课题的主要研究内容是输电线路行波故障测距,主要完成以下工作:
1)研究了行波在输电线路的传播过程、行波的相模变换原理、故障点反射波和对端母线反射波的识别原理,将小波变换运用于故障行波信息的提取、故障选线、故障选相算法,对传统的行波故障选相判据进行了修正。
2)在传统的行波测距原理基础上,推导出不受波速影响的测距算法,包括单端测距和双端测距,消除了由波速不确定而对测距结果造成的影响,以提高行波故障测距方法的精度;针对电缆-架空线混合线路研究了基于波速度归一的测距算法。
3)由于高频行波极易被噪声污染,在行波测距之前要对信号进行去噪处理,在仿真中将高斯白噪声和正负脉冲噪声加入无噪信号,再应用经验模态分解(EMD)进行行波去噪。
4)在Matlab/Simulink环境下搭建了参数均匀线路和电缆-架空线混合线路的电力系统模型,就各种短路故障进行仿真,对采集到的故障数据进行计算分析,以验证不受波速影响算法的有效性,同时验证去噪的效果。
2 输电线路行波测距理论
2.1 行波在输电线路上的传播
2.1.1 行波的波动方程
均匀无损导线等值电路如图2.1所示。
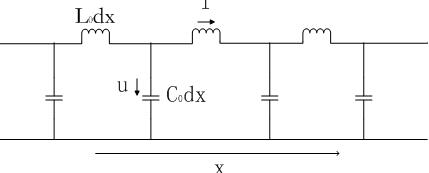
图2.1 均匀无损导线的等值电路