- 上一篇:激光超声无损检测粘结缺陷的研究现状
- 下一篇:薄膜厚度与折射率的测量方法研究
第四章简述了曲线跟踪算法并在matlab上得以实现。对用高速摄像机拍摄的光纤释放姿态曲线进行跟踪。
2 运用Radon变换进行图像处理
2.1 Radon变换背景及原理
Radon变换于1917年首先由Johann Radon建立[12],当时的工作集中在求取2D、3D物体特征的分布上,半个世纪后,用于数字图像上检测直线的Hough变换才被引入,因此有一种说法是Hough变换只是Radon变换的特例。Radon变换已经在数字图像领域取得了广泛的应用。在医学上CT图像建立的数学基础就是Radon变换[13];在识别领域由Radon变换域进行特征的判别更具鲁棒性[14]。图像投影,就是说将图像在某一方向上做线性积分或理解为累加求和。如果将图像看成二维函数f(x, y),则其投影就是在特定方向上的线性积分,比如f(x, y)在垂直方向上的线性积分就是其在x轴上的投影;f(x, y)在水平方向上的线积分就是其在y轴上的投影。通过这些投影,可以获取图像在指定方向上的突出特性这在图像模式识别等处理中可能会用到。Radon变换(拉东变换),就是将数字图像矩阵在某一指定角度射线方向上做投影变换。这就是说可以沿着任意角度theta来做Radon变换。图2.1为135°方向投影示意图。
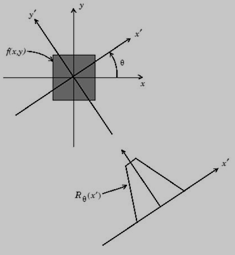
图2.1 在135°方向的投影
公式如下
可以用Radon变换来提取图像中直线.其原理是对原图像沿不同方向进行投影,并对投影结果建立二维直方图。选取极值点为直线所对应的点(二维直方图 中的每一个极值点的两坐标对应直线边缘的倾斜角度和位置,而该坐标处对应的函数值对应投影的高度),从而可以得到直线的几何参数信息 (倾斜角度和位置)。对于离散情形,在数学图像中就是把那些将沿某方向的像素相加,即投影到与该投影方向相垂直的轴线上。Radon变换可以理解为图像在极坐标空间的投影,极坐标空间的每一点对应一条直 线,而Radon变换是图像像素点在每一条直线上的积分。因此,图像中高灰度值的直线会在极坐标空间形成亮点,而低灰度值的线段在极坐标空间形成暗点。直线的检测转化为在变换域对亮点、暗点的检测[15]。
2.2 Radon变换的实现
本文的所有图像处理算法的实现都是基于matlab实现的。由于MATLAB中的绝大多数的运算都是通过矩阵这一形式进行的,这一特点也就决定了MATLAB在处理数字图像上的独特优势。理论上讲,图像是一种二维的连续函数,然而在计算机上对图像进行数字处理的时候,首先必须对其在空间和亮度上进行数字化,这就是图像的采样和量化的过程。二维图像进行均匀采样,就可得到一幅离散化成M×N样本的数字图像,该数字图像是一个整数阵列,因而用矩阵来描述该数字图像是最直观最简便的了,而MATLAB的长处就是处理矩阵运算,因此用MATLAB处理数字图像非常的方便[16]。来!自~751论-文|网www.751com.cn
由2.1节所介绍的Radon变换的原理,Radon变换的关键是要实现图像在任意角度直线上的线积分,也即过图像的任意直线所经像素点的灰度值累加。实现这一功能的方法有很多。下面是我在matlab上所采用的一种较简单的Radon变换实现方法。该种方法主要先对所要处理图片的每个像素点设定坐标值,再通过坐标关系:
进行插值运算。然后将插值结果像素点进行累加实现 角度的Radon变换。下图为Radon变换的实现流程图(具体代码见附件A):
Radon变换的实现算法流程图
2.3 本章小结